
In general, if we start looking for this second difference at the $n^$, then the first few terms are summarised below. Then the second-level differences are $(4-2),(6-4),\ldots$ and happen to always be $2$. The second difference being referred to is the difference between adjacent differences.

The difference between the first two terms comes from writing down the first and second terms and taking their difference: $(a*2^2+b*2+c)-(a*1^2+b*1+c) =a*3+b $ The first-term formula comes from substituting in $n=1$, since $n$ is the variable being used to denote which term we're looking at. "Quadratic" basically means $an^2+bn+c $ (historically related to things like "a square has four sides" and "quad is the Latin root for 'four'"), so that formula could be treated as true by the definition of "quadratic sequence". But it is easier to use this Rule: x n n (n+1)/2.

The Sequence Calculator finds the equation of the sequence and also allows you to view the next terms in the sequence. The coefficient of \(n^2\) is half the second difference, which is 2.For the formula, I think you may have the idea backwards. The Triangular Number Sequence is generated from a pattern of dots which form a triangle: By adding another row of dots and counting all the dots we can find the next number of the sequence. Step 1: Enter the terms of the sequence below. The second difference is the same so the sequence is quadratic and will contain an \(n^2\) term. Work out the \(n\) th term of the sequence 5, 11, 21, 35. Step 2 Move the number term to the right side of the equation: P 2 460P -42000. (Higher Only).This video is part of the Algebra module in GCS.
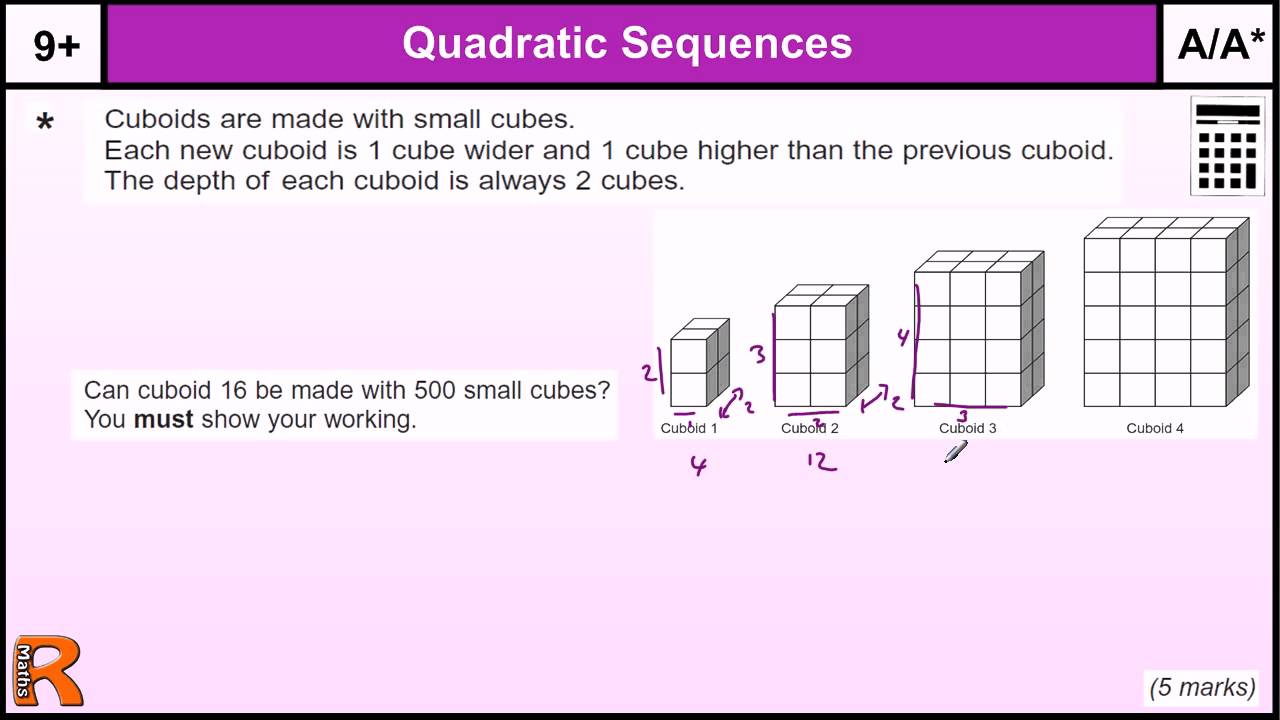
In this example, you need to add \(1\) to \(n^2\) to match the sequence. A video revising the techniques and strategies for finding the nth term of quadratic sequences. To work out the \(n\) th term of the sequence, write out the numbers in the sequence \(n^2\) and compare this sequence with the sequence in the question. Half of 2 is 1, so the coefficient of \(n^2\) is 1. (If a 0 and b 0 then the equation is linear, not quadratic. In this example, the second difference is 2. In algebra, a quadratic equation (from Latin quadratus ' square ') is any equation that can be rearranged in standard form as 1 where x represents an unknown value, and a, b, and c represent known numbers, where a 0. The coefficient of \(n^2\) is always half of the second difference. The sequence is quadratic and will contain an \(n^2\) term.

The first differences are not the same, so work out the second differences. The terms in the quadratic sequence appear in the linear sequence with an increasing number of terms between them - one number between the first two terms, then. Work out the first differences between the terms. We simply substitute n into the n th term rule for our. Remember, n stands for the position of the term: for the 1st term, n 1 for the 10th term, n 10 for the 1765th term, n 1765. Work out the \(n\) th term of the sequence 2, 5, 10, 17, 26. Finding any term in a quadratic sequence using an n th term rule: In any sequence, if you know the n th term rule, you can find any term in that sequence. They can be identified by the fact that the differences in between the terms are not equal, but the second differences between terms are equal. Quadratic sequences are sequences that include an \(n^2\) term.


 0 kommentar(er)
0 kommentar(er)
